Practice Reading Files and Plotting Data#

Creative Commons Licence

Author: Dr Antonia Mey and Dr James Cumby
Email: antonia.mey@ed.ac.uk, james.cumby@ed.ac.uk

Question 1#

  1. Read in data from extra/X_calibration.csv into a dataframe.

  2. Inspect the dataframe you have read in.

  3. Plot the absorbance vs. mass concentration data (in g dm\(^{-3}\)) of a compound X. Write a function that will plot this calibration curve (DataFrame taken as the function argument) as a scatter plot, with axes correctly labelled including units.

# Answer here

Question 2#

The radial part (\(R(r)\)) of the hydrogen wavefunction for the quantum numbers \(n\) and \(l\) is given by the equation $\( R(r) = \frac{2r}{na_0}\sum_{k=0}^{n-l-1} a_k \left( \frac{2r}{na_0} \right)^k \exp \left( {-\frac{r}{na_0}} \right) \)\( where the coefficient \)a_k\( is determined from a recursion relationship, \)\( a_{k+1} = \frac{k+l+1-n}{(k+1)(k+2l+2)}a_k \)\( and \)a_0$ is the Bohr radius.

Generally more useful for visualisation is the atomic radial distribution function $\( \mathrm{RDF} = 4 \pi r^2 R(r)^2 \)\( which readily shows the number of radial nodes for a given combination of \)(n, l)$.

The function atomic_rdf takes as its input the quantum numbers \(n\) and \(l\) and a maximum radius for which to calculate the rdf for (in units of \(a_0\), the Bohr radius) and returns two lists; the first of r distances (in \(a_0\) units) and the second of the calculated RDF at each point.

Write a function that will take an integer \(n\) as input (\(1 \leq n_{\mathrm{max}} \leq 4\)), and produce a plot of the RDFs for \(n = 1, 2 ..., n_\mathrm{max}\) containing the wavefunction with the fewest radial nodes for each \(n\). For example, \(n_{\mathrm{max}} = 3\) would produce a plot of the 1s, 2p and 3d RDFs.

Remember, the number of radial nodes for a given \(n,l\) pair is given by \(n - l - 1\).

Your function should incorporate assert statements to check that the input value is valid, and return the matplotlib axes object. Internally, call the atomic_rdf function to generate the necessary curves. Your plot should extend from \(0 a_0\leq r < 50 a_0\) and should have axes correctly labelled with the quantity plotted and any units.

Your plot should adopt the following formatting:

  • overall figure should have a width:height ratio of 1.618 (the ‘golden’ ratio)

  • The colours and line formats should be as follows:

    Principal quantum number \(n\)

    Line Colour

    1

    black (‘k’)

    2

    red (‘r’)

    3

    Matplotlib C1

    4

    Matplotlib C2

    5

    Matplotlib C3

    6 - 10

    Matplotlib C4 - C8

    Angular quantum number \(l\)

    Line Style

    0 (s)

    Solid line

    1 (p)

    Dashed line

    2 (d)

    dot-dash line

    3 (f)

    dotted line

    		 
# Answer here

Question 3#

The file data_sources/V_containing_ICSD.csv contains details of many of the reported crystal structures containing vanadium.

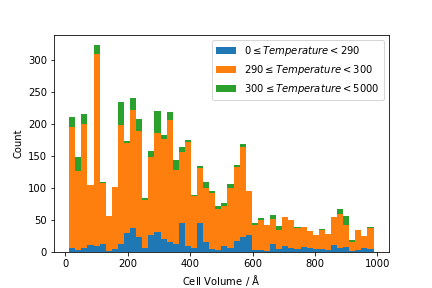
plot_icsd is intended to take a data file with the same format as V_containing_ICSD.csv, and produce a histogram based on the CellVolume column values. In addition, it takes two arguments (groupby_col and group_ranges) which should cause it to create a stacked histogram based on data in another column. For example, if groupby_col = Temperature then plot_icsd should produce a plot where histograms for different temperature ranges are stacked on top of each other. The ranges to use are defined by the group_ranges argument, which is a list containing the temperature divisions. These ranges should be exclusive of the upper value, but inclusive of the lower value, i.e.

group_ranges = [0, 290, 300, 5000] should produce three sets of bars, with the data distributed as: $\( 0 \leq T < 290 \\ 290 \leq T < 300 \\ 300 \leq T < 5000 \\ \)$

By way of an example, plot_icsd('data_sources/V_containing_ICSD.csv', 'Temperature', [0, 290, 300, 5000]) should produce a plot similar to the following: Example CellVolume histogram

Points to note#

  • If groupby_col == '' or group_ranges is an empty list, plot_icsd should return a simple (non-stacked) histogram

  • You should use 50 histogram bins distributed across the full range of the CellVolume values.

    Hint: to generate an certain number of bins across a range, use np.linspace(start, end, number_of_bins+1) (remember that computing a histogram requires both left and right edges of each bin, but plotting only requires the left edge)

  • The width of the plotted bins should be the correct size for the data

    Hint: np.linspace can also return the step size if asked…

  • Remember to stack the bars, and not just plot them starting from zero.

  • Remember to add a legend and meaningful axis labels, based on the data received.