Unit 05: Introduction to NumPy and Plotting, part I#

Authors:

Dr Valentina Erastova
Dr Matteo Degiacomi
Hannah Pollak

Email: valentina.erastova@ed.ac.uk

Learning objectives #

use the numpy library
perform mathematical operations on numpy arrays in 1D and in 2D
access parts of arrays
load arrays to or from files

Some of the material was adapted from Python4Science.

Table of Contents#

Arrays and NumPy
1.1 1D Arrays
1.2 Tasks 1
Mathematical operations on 1D arrays
Accessing slices of 1D arrays
Multidimensional arrays
4.1 Generating 2D arrays
4.2 Slicing 2D arrays
4.3 Tasks 2
Mathematical operations on multidimensional arrays
Next notebook

Jupyter Cheat Sheet

To run the currently highlighted cell and move focus to the next cell, hold ⇧ Shift and press ⏎ Enter;
To run the currently highlighted cell and keep focus in the same cell, hold ⇧ Ctrl and press ⏎ Enter;
To get help for a specific function, place the cursor within the function’s brackets, hold ⇧ Shift, and press ⇥ Tab;

Links to documentation#

You can find useful information about using numpy and matplotlib at

1. Arrays and NumPy #

An array is a smart way of storing multidimensional numerical data.
NumPy, which stands for Numerical Python, is a module consisting of multidimensional array objects and a collection of routines for processing those arrays.
We can use NumPy to perform mathematical and logical operations on arrays.
NumPy is a base for many other modules, including Pandas, and so they can be used together.

Import the NumPy library#

For NumPy, the standard-practice alias is np.:

import numpy as np

1.1 1D Arrays #

NumPy arrays can only contain one datatype, i.e. all integers, all floats, etc. This is in contrast to lists, which can contain a mix of datatypes.

Creating 1D arrays#

To create an array of integers (single numbers like 1, 2, 3, 4, 5) we can do it by converting a list to an array as:

import numpy as np

my_list = [1, 2, 3, 4, 5]

my_array = np.array(my_list)

Example 1#

# Create a 1D numpy array:

# FIXME

Click here to see the solution to Example 1.

a = [1, 2, 3, 4, 5] # Your list can be of any length
my_array = np.array(a)

Example 2#

Let’s look at some of the properties of our array.

How do you get the dimensions, shape, size, and data type of an array?

# Create a 1D array

# Check the properties of this 1D array

# dimensions?

# shape?

# size? 

# data type?

Click here to see the solution to Example 2.

# Create a 1D array
a = [1, 2, 3, 4, 5]
my_array = np.array(a)

# Check the properties of this 1D array
print(f"Dimensions {my_array.ndim}")
print(f"Shape {my_array.shape}")
print(f"Size {my_array.size}")
print(f"Datatype {my_array.dtype}")

Example 3#

We can also use functions to generate arrays.

Similarly to the built-in function range, we can generate one-dimensional arrays of equally-spaced numbers with:

np.linspace(start, end, quantity) or
np.arange(start, end, step_size)

We can also generate multidimensional arrays filled with zeros or ones with NumPy functions:

np.zeros(shape)
np.ones(shape)

where shape has to be an int for 1D arrays and tuple, such as (5, 6), for creating a 2D array.

Let’s use np.zeros(shape) to create a 1D array full of zeros:

# FIXME

Click here to see the solution to Example 4.

z = np.zeros(10)
print(f"My array of zeros {z} is of type {z.dtype}")

Tasks 1 #

We will continue to generate 1D arrays, access parts of an array, and perform some mathematical operations on them.

Task 1.1 : Generate a 1D array of length 5, filled with ones.

# FIXME

Click here to see the solution to Task 1.1

ones = np.ones(5)
print(f"Array of five ones: {ones}")

Task 1.2: Create an array with `np.arange`

Using np.arange, create a 1D array as a sequence from 0 to 20 in steps of 2.

# FIXME

Click here to see the solution to Task 1.2

sequence = np.arange(0, 21, 2) 
print(sequence)

Question: What number did you have to stop at to include 20 as a last number? Why?

Click here to see the answer to the above question.

Python starts counting from 0 and in np.arange(start, stop, step), the stop value is not inclusive.

Advanced Task 1.3

Find the last number in an array np.arange(0, 20, 2).

Is the answer as you expected?

# FIXME

Click here to see the solution to the Advanced task 1.3.

a = np.arange(0, 20, 2)
last = a[-1]
print(last)

Task 1.4: Generate another array

Generate the same array as we did with np.arange(0, 20, 2) but this time using np.linspace(start, stop, n_steps).

How do these two functions differ?

# FIXME

Click here to see the solution to Task 1.4

b = np.linspace(0, 20, 11)
print(b)

Note that in this case, the end point is included in the generated array. This is also explained in the documentation.

2. Mathematical operations on 1D arrays #

All mathematical operations between NumPy arrays act element by element. This is not the same for lists, which is why using NumPy is so useful.

Operations with scalar numbers act on every element of the array.

For example:

If we define:

a = np.array([1, 2, 3])
b = np.array([0, 1, 2])

then

a * b returns the array [0, 2, 6]
a - b returns the array [1, 1, 1]
a + 1 returns the array [2, 3, 4]

Arrays can be used to conduct mathematical operations in a compact way. If we were using lists, we would have to loop through each element of the list to perform similar operations.

We will see some examples of this below.

Task 2.1: Add a scalar to an array

Create an array called my_array containing the numbers 3, 6, 7, 2 and 8. Add the number 3 to every number of the array.

# FIXME

Click here to see the solution to Task 2.1

my_array = np.array([3, 6, 7, 2, 8])

new_array = my_array + 2

print(f"my_array + 3 = {new_array}")

We can also do mathematical operations between two arrays.

Note: the arrays have to have the same dimensions.

Task 2.2: Mathematical operations between two arrays.

Create 2 arrays of your liking and perform mathematical operations.

For example: multiply them, substract one from another, and add them up.

Print the answers.

# FIXME
a = 
b = 

print(f"multiplication a * b = {___}")
print(f"substraction a - b = {___}")
print(f"addition a + b = {___}")

Click here to see solution to Task 2.2

a = np.array([1, 2, 4])
b = np.array([0, 1, 2])

print(f"multiplication a * b = {a * b}")
print(f"substraction a - b = {a - b}")
print(f"addition a + b = {a + b}")

Task 2.3: Square each value in my_array

Hint: you can use ** as an operator to raise to a power, i.e. $x^2$ would be written as x**2 in Python.

# FIXME

Click here to see the soluton to Task 2.3.

my_array = np.array([3, 6, 7, 2, 8])
my_array_squared = my_array ** 2

print(my_array_squared)

Example 4#

What is the difference between using numpy and using math?

How do you calculate:

the square-root of a single number?
the square-root of a list?
the square-root of an array?

See what happens when you run the code below.

Note: The community-agreed alias for the math library is just m.

import math as m
import numpy as np

# Square-root of a single number:
# with math
print (m.sqrt(4)) 
# with numpy
print (np.sqrt(4))
# mathematically, by calculating 4^{1/2} 
print (4**0.5) 

# Square-root of a list of numbers
l = [4, 9, 16] 
# numpy: square root of every element 
print (np.sqrt(l)) 
 # Can you use math here?
print (m.sqrt(l)) 

# Square-root of an array
a = np.array(l)
# square root of every element of a numpy array
print(np.sqrt(a)) 
# would this work?
print(m.sqrt(a)) 

3. Accessing slices of 1D arrays #

Slicing an array is the operation of extracting a subset of it, as shown in the figure below.

We will learn about slicing in the following task.

Task 3.1: Slicing arrays

Generate a 1D array of 20 elements and fill it with random numbers.
Pick every 3rd value within the first 10 values.
Print how many values you get
What is the last number in your array? (See Advanced task 1.3)

Hint

Try executing np.random.default_rng(seed)

This is a random number generator, where the seed is used to “initialise” the number generator. You can read more about this in the Random Generator Documentation from NumPy.

# 1. Generate a 1D array of 20 elements and fill it with random numbers.
# FIXME

# 2. Pick every 3rd value within the first 10 values.
# FIXME

# 3. Print how many values you get
# FIXME

# 4. What is the last number in your array?
# FIXME

Click here to see the solution to Task 3.1.

# 1. Generate a 1D array of 20 elements and fill it with random numbers.

random_generator = np.random.default_rng(12345)
random_numbers = random_generator.random(20)
print(random_numbers)

# 2. Pick every 3rd value within the first 10 values.
picked = random_numbers[0:10:3]

# 3. Print how many values you get
print(len(random_numbers))
print(len(picked))

# 4. What is the last number in your array?    
last = random_numbers[-1]
print(last)

4. Multidimensional arrays #

4.1 Generating 2D arrays #

Just like with 1D arrays, we can also create a 2D array in the following manner:

a = [[1, 2], [3, 4], [5, 6]]
my_2d_array = np.array(a)

Sometimes it’s nice to write out the array in separate lines to see the columns and the rows more clearly. However, it doesn’t change the way Python sees the array.

a = [[1, 2], 
     [3, 4], 
     [5, 6]]
my_2d_array = np.array(a)

Note: to create a 2D array, we pass a "list of lists" to numpy's array method. Each "inner list" describes a row, all inner lists should have the same length. For a 3D array, we would pass a "list of lists of lists", and so on.

Example 5#

Create a two-dimensional array.

# FIXME

Click here to see solution to Example 5.

b = [[1, 2], [3, 4], [5, 6]]
my_2d_array = np.array(b)

print(my_2d_array)

Question: What is the difference between tuple, array, and list?

Click here to see Answer.

List: A list is of an ordered collection data type that is mutable which means it can be easily modified and we can change its data values and a list can be indexed, sliced, and changed and each element can be accessed using its index value in the list. The following are the main characteristics of a List:

The list is an ordered collection of data types.
The list is mutable.
List are dynamic and can contain objects of different data types.
List elements can be accessed by index number.

list = ["mango", "strawberry", "orange",
		"apple", "banana"]
print(list)

# we can specify the range of the
# index by specifying where to start
# and where to end
print(list[2:4])

# we can also change the item in the
# list by using its index number
list[1] = "grapes"
print(list[1])

Array: An array is a collection of items stored at contiguous memory locations. The idea is to store multiple items of the same type together. This makes it easier to calculate the position of each element by simply adding an offset to a base value, i.e., the memory location of the first element of the array (generally denoted by the name of the array). The following are the main characteristics of an Array:

An array is an ordered collection of the similar data types.
An array is mutable.
An array can be accessed by using its index number.

# importing "array" for array creations
import array as arr

# creating an array with integer type
a = arr.array('i', [1, 2, 3])

# printing original array
print ("The new created array is : ", end =" ")
for i in range (0, 3):
	print (a[i], end =" ")
print()

# creating an array with float type
b = arr.array('d', [2.5, 3.2, 3.3])

Tuple: A tuple is an ordered and an immutable data type which means we cannot change its values and tuples are written in round brackets. We can access tuple by referring to the index number inside the square brackets. The following are the main characteristics of a Tuple:

Tuples are immutable and can store any type of data type.
it is defined using ().
it cannot be changed or replaced as it is an immutable data type.

tuple = ("orange","apple","banana")
print(tuple)

# we can access the items in
# the tuple by its index number
print(tuple[2])

#we can specify the range of the
# index by specifying where to start
# and where to end
print(tuple[0:2])

Taken from www.geeksforgeeks.org

Array properties of 2D arrays#

Consider the array

a = [[0, 1, 2, 3],
     [10, 11, 12, 13],
     [20, 21, 22, 23]]

The number of dimensions or axes of the array is given by a.ndim and in this case returns 2
The shape of the array, i.e. the size of each dimension is given by a.shape, which returns a tuple (3, 4)
The size of the array, i.e. the total number of elements in the array is given by a.size, which returns 12
The datatype of each element is given by a.dtype, which returns int64

Example 6#

Print the number of dimensions, shape and size of my_2d_array from above.

# FIXME

Click here to see the solution to Example 6.

print(f"dimension: {my_2d_array.ndim}")
print(f"shape: {my_2d_array.shape}")
print(f"size: {my_2d_array.size}")

Note how in the example above, the shape of the matrix is defined as (rows, columns) - the number of rows and then columns.

The output of shape is written in round brackets, i.e. it is a tuple and is non-changeable.

Example 7#

Let’s try to create an array filled with predefined values and check it’s properties.

We can use np.ones to fill it with ones, or np.zeros to fill up an array with zeros. If we want to use a specific value to fill an array with, we can use the function np.full.

Generate an array of shape (4, 5) filled with the number 1.234.

# FIXME

Click here to see solution to Example 7.

# Generate an array of 4 x 5 filled up with a 1.234
f = np.full((4, 5), 1.234)

# Check its properties
print(f"Dimensions {f.ndim}")
print(f"shape {f.shape}")
print(f"Size {f.size}")

4.2 Slicing 2D arrays #

We can access data in a multidimensional array by slicing it, in a similar way to 1D arrays:

Example 8#

Create an array of shape (5, 7) filled with random integers.

We can again use np.random.default_rng(seed) to generate a random number generator and generator.integers(low, high, size) to generate an array filled with random numbers.

# FIXME

Click here to see the solution to Example 8.

number_generator = np.random.default_rng(12345)
random_big_array = number_generator.integers(low=1, high=50, size=(5, 7))

print(random_big_array)

Example 9#

Use slicing on random_big_array to select:

the first column
the last column
the 4th row
an area
samples in a given space

# FIXME

Click here to see the solution to Example 9.

print(f"first column {random_big_array[:, 0]}")
print(f"last column {random_big_array[:, -1]}")
print(f"4th row {random_big_array[3, :]}")
print(f"selected area {random_big_array[0:2, 3:7]}")
print(f"samples {random_big_array[1:5:2, 3:10:3]}")

Loading an array to/from a file #

As you have seen before using pandas, we can also load arrays from a plain text file.

There are many options available for loading the file, such as:

To load a file array.txt:

loaded_array = np.loadtxt("array.txt")

We can skip some lines, for example in the case where the file has a header over the first 5 lines of the file, using the option skiprows.

Similarly, if the file contains comments, we can use the option comments to specify the character used for comments, so that these lines also get ignored by python.

clean_array = np.loadtxt("array.txt", comments="#", skiprows=5)

To save the array called my_array into the file, use np.savetxt:

np.savetxt("my_array.txt", data)

Task 4.1: Load data to and from a file with arrays

Load in the file data/slice_me.txt and skip the first row. (The data/ part specifies the folder in which the file is.)
Print the shape of this data
Save this to another file called data/slice_me_copy.txt

# 1. Load in the file data/slice_me.txt and skip the first row.
# FIXME

# 2. Print the shape of this data
# FIXME

# 3. Save this to another file called data/slice_me_copy.txt
# FIXME

Click here to see the solution to Task 4.1

# 1. Load in the file data/slice_me.txt and skip the first row.
data = np.loadtxt("data/slice_me.txt", skiprows=1)

# 2. Print the shape of this data
print(data.shape)

# 3. Save this to another file called data/slice_me_copy.txt
np.savetxt("data/slice_me_copy.txt", data)

Task 4.2: Slicing data arrays

The folder data contains a file called ms.txt, which contains mass spectrometry data given in two columns: m/z and intensity.

Read in the file ms.txt
Create a sub-sample of the intensities data by extracting every 10th line into a variable called subdata.
Save the subdata into a new file.

Note: it might be a good idea to print the shapes of data and subdata to check if your slicing is correct after step 2.

# 1. Read in the file ms.txt
# FIXME

# 2. Create a sub-sample of the data by extracting every 10th line into a variable called `subdata`.
# FIXME

# 3. Save the intensities column from `subdata` into a new file.
# FIXME

Click here to see the solution to Task 4.2.

# 1. Read in the file ms.txt
data = np.loadtxt("data/ms.txt")

# 2. Create a sub-sample of the data by extracting every 10th line into a variable called `subdata`.
subdata = data[::10, 1]

# Check the shapes of the datasets
print(data.shape)
print(subdata.shape)

# 3. Save the intensities column from `subdata` into a new file.
np.savetxt("data/sub_intensities.txt", subdata)

Advanced Task 4.3

Can you do the above without numpy, only using in-built python functionality?

# FIXME

Click here to see the solution to the Advanced task 2.4

# Read file in line by line
with open("data/ms.txt", "r") as input_file:
    lines = input_file.readlines()

# Counter for counting every 10th line
counter = 0

# Create an empty list to store intensity values
intensities = []

# Loop over the lines in the file
for line in lines:

    # If counter is divisible by 10
    if counter % 10 == 0:
        # split the line (string) into two columns:
        columns = line.split()

        # the second column is intensity
        intensity = columns[1]

        # append intensity value to intensities list
        intensities.append(intensity)

    # increment the counter
    counter += 1

# Open file for writing:
with open("data/sub_densities.txt", "w") as output_file:
    # Loop over all the values in the list intensities
    for intensity in intensities:
        # Write each intensity to the file on separate lines
        output_file.write(f"{intensity} \n")

5. Mathematical operations on multidimensional arrays #

all the algebraic operations described in Section 2 for 1D arrays, also apply to n-dimensional arrays.

⚠️ Arrays do not behave like matrices. All mathematical operations between arrays of any shape act element by element (similarly to 1D arrays).

Let’s start by defining a 2D array.

my_list = [[0, 1, 2, 3],
           [10, 11, 12, 13],
           [20, 21, 22, 23]]
my_array = np.array(my_list)

Numpy provides a range of methods to extract information from your numerical data. For instance, to sum all the values in the array you can use th np.sum(a) method (where a is an array):

total_sum = np.sum(my_array) 
print(total_sum)

This prints 138.

Besides sum, numpy offers many other useful methods to extract information from numerical data, for instance:

np.min(a) find the minimum value in the array
np.argmin(a) find position (AKA index) of the minimum value in the array
np.max(a) find maximum value in the array
np.argmax(a) find position (AKA index) of the maximum value in the array
np.unique(a) selects a subset of unique elements
np.sort(a) sorts the array from the maximum to the minimum value
np.mean(a) and numpy.std(a) compute mean and standard deviation of array values
np.median(a) computes the median value of an array.

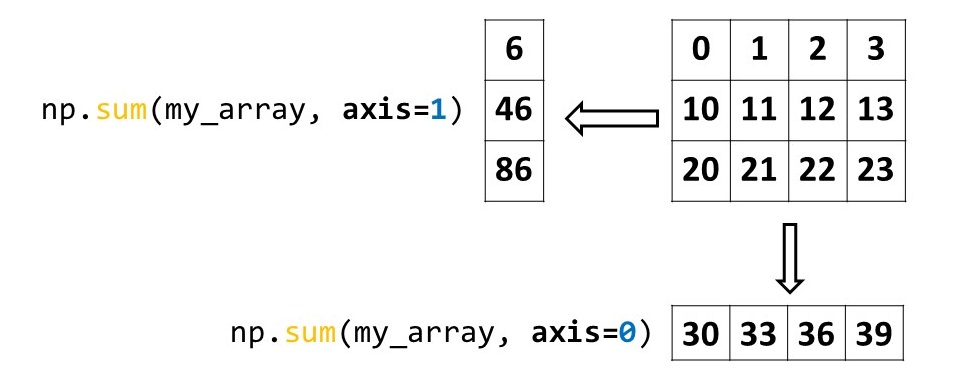
Axis of operations#

What if we want to get the sum of elements, row by row? We can define the axis of operation as follows:

row_sum = np.sum(my_array, axis=0)
print(row_sum)

This prints [30, 33, 36, 39].

Similarly, to get the sum of elements, column by column:

column_sum = np.sum(my_array, axis=1)
print(column_sum)

This prints [6, 46, 86].

The following figure displays a graphical representation of what we just did.

Task 5.1: Sum of array elements

Calculate the sum of all the elements in the file data/slice_me_copy.txt that you created in Task 4.1.
Calculate the “vertical sum”, i.e. the sum along the rows.
Calculate the “horizontal sum”, i.e. the sum along the columns.

# 1. Calculate the sum of all the elements in the file `data/slice_me_copy.txt` that you created in the previous task.
# FIXME

# 2. Calculate the "vertical sum", i.e. the sum along the rows.
# FIXME

# 3. Calculate the "horizontal sum", i.e. the sum along the columns.
# FIXME

Click here to see the solution to Task 5.1

array = np.loadtxt("data/slice_me_copy.txt")

# 1. Calculate the sum of all the elements in the file `data/slice_me_copy.txt` that you created in the previous task.
total_sum = np.sum(array)
print(f"total sum {total_sum}")

# 2. Calculate the "vertical sum", i.e. the sum along the rows.
vertical_sum = np.sum(array, axis=0)
print(f"vertical sum {vertical_sum}")

# 3. Calculate the "horizontal sum", i.e. the sum along the columns.
horizontal_sum = np.sum(array, axis=1)
print(f"horizontal sum {horizontal_sum}")

Advanced Task 5.2

Using the mass spectrometry data in the file ms.txt we previously studied in Task 4.2, find the m/z values in the region between 6400 and 6600.

Also find the maximum peak value in this region and the corresponding m/z value.

Hint: You will need to use Boolean indexing. This was covered in Unit 03 Part II

# FIXME

Click here to see the solution to Advanced task 5.2

# Load in data
data = np.loadtxt("data/ms.txt")

# Create criterion
greater_than = data[:,0] > 6400
less_than = data[:, 0] < 6600
criterion = greater_than & less_than

# slice the array
sliced_array = data[criterion, :]

# Get the maximum peak value
maximum_value = np.max(sliced_array[:, 1])
index_of_max = np.argmax(sliced_array[:, 1])
mz_at_max = sliced_array[index_of_max, 0]

print(f"peak {maximum_value} is at m/z {mz_at_max}")

Key Points #

Numpy is a Python package to efficiently read/write and manipulate numerical data
it can handle data of arbitrary size and shape
algebraic operations across arrays take place element by element, i.e. arrays are not matrices.
numpy enables applying mathematical operations along desider axes.

Next notebook#

Unit 05 II_plotting

Data-Driven Chemistry

Unit 05: Introduction to NumPy and Plotting, part I

Contents